7  Word Embedding

Text als Datenbasis prädiktiver Modelle Bild von mcmurryjulie auf Pixabay

7.1 Vorab

7.1.1 Lernziele

  • Die Erstellung von Word-Embeddings anhand grundlegender R-Funktionen erläutern können.

7.1.2 Begleitliteratur

Arbeiten Sie Hvitfeldt und Silge (2021), Kap. 5 vor dem Unterricht durch als Vorbereitung.

7.1.3 Benötigte R-Pakete

library(tidyverse)
library(easystats)  # Komfort fĂĽr deskriptive Statistiken, wie `describe_distribution`
library(tidytext)
library(hcandersenr)   # Textdaten
library(slider)  # slide
library(widyr)  # pairwise_pmi
library(furrr)  # mehrere Kerne gleichzeitig nutzen
library(textdata)  # Worteinbettungen wie Glove6b, vorgekocht
library(entropy)  # Entropie berechnen
library(widyr)  # Ă„hnlichkeit berechnen mit widyr_svd
library(furrr)  # Mehrere Kerne gleichzeitig

7.2 Daten

7.2.1 Complaints-Datensatz

Der Datensatz complaints stammt aus dieser Quelle.

Den Datensatz complaints kann man hier herunterladen. Im Buch ist die Webseite nicht (direkt?) angegeben. Die Datei ist mit gz gepackt; read_csv sollte das automatisch entpacken. Achtung: Die Datei ist recht groĂź.

d_path <- "https://github.com/EmilHvitfeldt/smltar/raw/master/data/complaints.csv.gz"
complaints <- read_csv(d_path)

Geschickter als jedes Mal die Datei herunterzuladen, ist es, sie einmal herunterzuladen, und dann lokal zu speichern, etwa im Unterordner data des RStudio-Projektordners.

Nach dem Importieren wird der Datensatz in eine Tidy-Form gebracht (mit unnest_tokens) und dann verschachtelt, mit nest.

7.2.2 Complaints verkĂĽrzt und geschachtelt

Um ein Herumprobieren zu erleichtern, ist hier der Datensatz complaints in zwei verkĂĽrzten Formen bereitgestellt:

nested_words2_path <- "https://github.com/sebastiansauer/datascience-text/raw/main/data/nested_words2.rds"
nested_words3_path <- "https://github.com/sebastiansauer/datascience-text/raw/main/data/nested_words3.rds"

nested_words2 enthält die ersten 10% des Datensatz nested_wordsund ist gut 4 MB groß (mit gz gezippt); er besteht aus ca. 11 Tausend Beschwerden. nested_words3 enthält nur die ersten 10 Beschwerden, was ihn gut zum Handhaben macht.

Beide sind verschachtelt und aus tidy_complaints (s. Kap. 5.1) hervorgegangen.

nested_words3 <- read_rds(nested_words3_path)

Das sieht dann so aus:

nested_words3 %>% 
  head(3)

Werfen wir einen Blick in den TExt der ersten Beschwerde des Datensatzes mit der ID nested_words3_path$complaint_id[1].

beschwerde1_text <- nested_words3$words[[1]]

Das ist ein Tibble mit einer Spalte und 17 Wörtern; da wir schon auf Unigramme aufgeteilt haben, ist jedes Wort ein Element des Vektors word:

beschwerde1_text %>% 
  head()
beschwerde1_text$word
##  [1] "systems"    "inc"        "is"         "trying"     "to"        
##  [6] "collect"    "a"          "debt"       "that"       "is"        
## [11] "not"        "mine"       "not"        "owed"       "and"       
## [16] "is"         "inaccurate"

7.3 Wordembeddings selber erstellen

7.3.1 PMI berechnen

Rufen Sie sich die Definition der PMI ins Gedächtnis, s. Gleichung eq-pmi.

Mit R kann man die PMI z.B. so berechnen, s. ? pairwise_pmi aus dem Paket widyr.

Zum Paket widyr von Robinson und Silge:

This package wraps the pattern of un-tidying data into a wide matrix, performing some processing, then turning it back into a tidy form. This is useful for several mathematical operations such as co-occurrence counts, correlations, or clustering that are best done on a wide matrix.

Quelle

Erzeugen wir uns Dummy-Daten:

dat <- tibble(feature = rep(1:5, each = 2),
              item = c("a", "b",
                       "a", "c",
                       "a", "c",
                       "b", "e",
                       "b", "f"))

dat

Aus der Hilfe der Funktion:

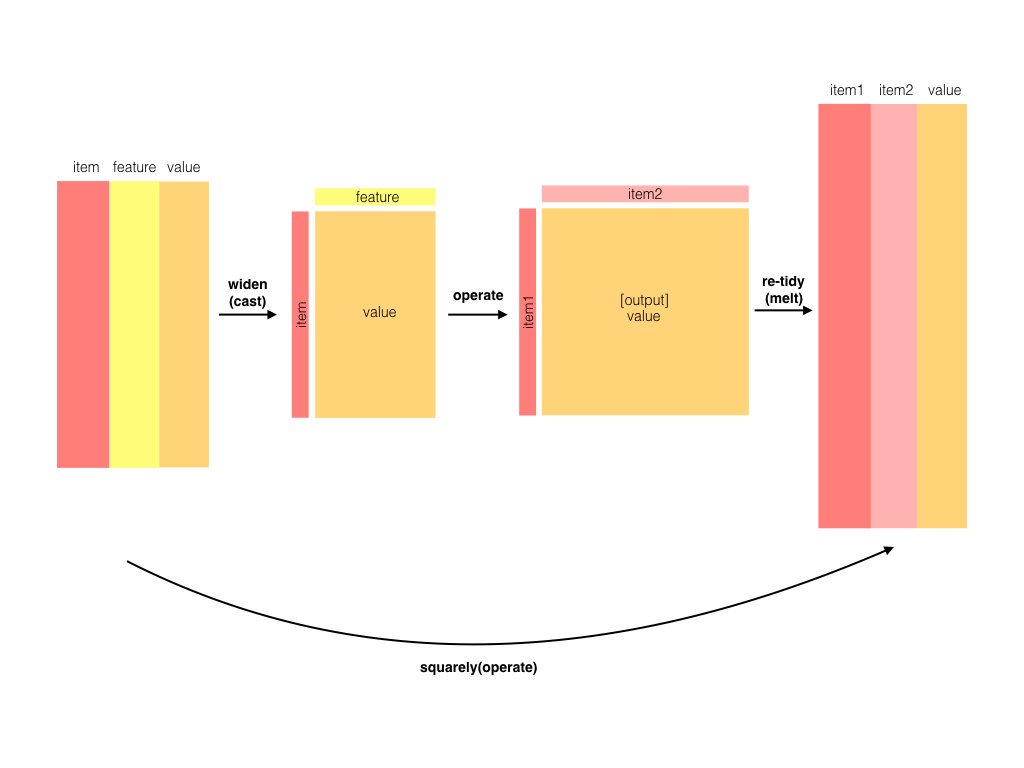
Find pointwise mutual information of pairs of items in a column, based on a “feature” column that links them together. This is an example of the spread-operate-retidy pattern.

Die Argumente der Funktion sind:

item

Item to compare; will end up in item1 and item2 columns

feature

Column describing the feature that links one item to others

Manche Berechnungen (Operationen) lassen sich vielleicht leichter nicht in der Tidy-Form (Langform), sondern in der “breiten” oder Matrixform ausführen. Wandeln wir mal dat von der Langform in die Breitform um:

table(dat$item, dat$feature)
##    
##     1 2 3 4 5
##   a 1 1 1 0 0
##   b 1 0 0 1 1
##   c 0 1 1 0 0
##   e 0 0 0 1 0
##   f 0 0 0 0 1

Silge und Robinson verdeutlichen das Prinzip von widyr so, s. Abbildung fig-widyr.

Abbildung 7.1: Die Funktionsweise von widyr, Quelle: Silge und Robinson

(Vgl. auch die Erklärung hier.)

Bauen wir das mal von Hand nach.

Randwahrscheinlichkeiten von a und c sowie deren Produkt, p_a_p_c:

p_a <- 3/5
p_c <- 2/5

p_a_p_c <- p_a * p_c
p_a_p_c
## [1] 0.24

Gemeinsame Wahrscheinlichkeit von a und c:

p_ac <- 2/5

PMI von Hand berechnet:

log(p_ac/p_a_p_c)
## [1] 0.5108256

Man beachte, dass hier als Basis \(e\), der natĂĽrliche Logarithmus, verwendet wurde (nicht 2).

Jetzt berechnen wir die PMI mit pairwise_pmi.

pairwise_pmi(dat, item = item, feature = feature)

Wie man sieht, entspricht unserer Berechnung von Hand der Berechnung mit pairwise_pmi.

7.3.2 Sliding

Sliding ist ein interessantes Konzept, aber man braucht vielleicht etwas Zeit, um sein Hirn um das Konzept zu wickeln…

Hier eine Illustration:

txt_vec <- "Das ist ein Test, von dem nicht viel zu erwarten ist"

slider::slide(txt_vec, ~ .x, .before = 2)
## [[1]]
## [1] "Das ist ein Test, von dem nicht viel zu erwarten ist"

Oh, da passiert nichts?! Kaputt? Nein, wir mĂĽssen jedes Wort als ein Element des Vektors auffassen.

txt_df <-
  tibble(txt = txt_vec) %>% 
  unnest_tokens(input = txt, output = word)

head(txt_df)
slider::slide(txt_df$word, ~ .x, .before = 2)
## [[1]]
## [1] "das"
## 
## [[2]]
## [1] "das" "ist"
## 
## [[3]]
## [1] "das" "ist" "ein"
## 
## [[4]]
## [1] "ist"  "ein"  "test"
## 
## [[5]]
## [1] "ein"  "test" "von" 
## 
## [[6]]
## [1] "test" "von"  "dem" 
## 
## [[7]]
## [1] "von"   "dem"   "nicht"
## 
## [[8]]
## [1] "dem"   "nicht" "viel" 
## 
## [[9]]
## [1] "nicht" "viel"  "zu"   
## 
## [[10]]
## [1] "viel"     "zu"       "erwarten"
## 
## [[11]]
## [1] "zu"       "erwarten" "ist"

Ah!

Das Aufteilen in einzelne Wörter pro Element des Vektors könnte man auch so erreichen:

txt_vec2 <- str_split(txt_vec, pattern = boundary("word")) %>% 
  simplify() 

slide(txt_vec2, .f = ~.x, .before = 2)
## [[1]]
## [1] "Das"
## 
## [[2]]
## [1] "Das" "ist"
## 
## [[3]]
## [1] "Das" "ist" "ein"
## 
## [[4]]
## [1] "ist"  "ein"  "Test"
## 
## [[5]]
## [1] "ein"  "Test" "von" 
## 
## [[6]]
## [1] "Test" "von"  "dem" 
## 
## [[7]]
## [1] "von"   "dem"   "nicht"
## 
## [[8]]
## [1] "dem"   "nicht" "viel" 
## 
## [[9]]
## [1] "nicht" "viel"  "zu"   
## 
## [[10]]
## [1] "viel"     "zu"       "erwarten"
## 
## [[11]]
## [1] "zu"       "erwarten" "ist"

In unserem Beispiel mit den Beschwerden:

slide(beschwerde1_text$word,  ~.x, .before = 2)
## [[1]]
## [1] "systems"
## 
## [[2]]
## [1] "systems" "inc"    
## 
## [[3]]
## [1] "systems" "inc"     "is"     
## 
## [[4]]
## [1] "inc"    "is"     "trying"
## 
## [[5]]
## [1] "is"     "trying" "to"    
## 
## [[6]]
## [1] "trying"  "to"      "collect"
## 
## [[7]]
## [1] "to"      "collect" "a"      
## 
## [[8]]
## [1] "collect" "a"       "debt"   
## 
## [[9]]
## [1] "a"    "debt" "that"
## 
## [[10]]
## [1] "debt" "that" "is"  
## 
## [[11]]
## [1] "that" "is"   "not" 
## 
## [[12]]
## [1] "is"   "not"  "mine"
## 
## [[13]]
## [1] "not"  "mine" "not" 
## 
## [[14]]
## [1] "mine" "not"  "owed"
## 
## [[15]]
## [1] "not"  "owed" "and" 
## 
## [[16]]
## [1] "owed" "and"  "is"  
## 
## [[17]]
## [1] "and"        "is"         "inaccurate"

7.3.3 Funktion slide_windows

Die Funktion slide_windows im Kapitel 5.2 ist recht kompliziert. In solchen Fällen ist es hilfreich, sich jeden Schritt einzeln ausführen zu lassen. Das machen wir jetzt mal.

Hier ist die Syntax der Funktion slide_windows:

slide_windows <- function(tbl, window_size) {
  skipgrams <- slider::slide(
    tbl, 
    ~.x,  # Syntax ähnlich zu purrr::map()
    .after = window_size - 1, 
    .step = 1, 
    .complete = TRUE
  )
  
  safe_mutate <- safely(mutate)
  
  out <- map2(skipgrams,
              1:length(skipgrams),
              ~ safe_mutate(.x, window_id = .y))
  
  out %>%
    transpose() %>%
    pluck("result") %>%
    compact() %>%
    bind_rows()
}

Erschwerend kommt eine große Datenmenge und eine lange Berechnungszeit dazu, was das Debuggen (Nachvollziehen und Durchdenken) der Schritte zusätzlich erschwert. In solchen Fällen hilft die goldene Regel: Mach es dir so einfach wie möglich (aber nicht einfacher). Wir nutzen also den stark verkleinerten Datensatz nested_words3, den wir oben importiert haben.

Zuerst erlauben wir mal, dasss unsere R-Session mehrere Kerne benutzen darf.

plan(multisession)  ## for parallel processing

Die Funktion slide_windows ist recht kompliziert. Es hilft oft, sich mit debug(fun) eine Funktion Schritt fĂĽr Schritt anzuschauen.

Gehen wir Schritt fĂĽr Schritt durch die Syntax von slide_windows.

Werfen wir einen Blick in words, erstes Element (ein Tibble mit einer Spalte). Denn die einzelnen Elemente vonwordswerden an die Funktionslide_windows` als “Futter” übergeben.

futter1 <- nested_words3[["words"]][[1]]
futter1

Das ist der Text der ersten Beschwerde.

Okay, also dann geht’s los durch die einzelnen Schritte der Funktion slide_windows.

Zunächst holen wir uns die “Fenster” oder “Skipgrams”:

skipgrams1 <- slider::slide(
   futter1, 
    ~.x, 
    .after = 3, 
    .step = 1, 
    .complete = TRUE
  )

Bei slide(tbl, ~.x) geben wir die Funktion an, die auf tbl angewendet werden soll. Daher auch die Tilde, die uns von purrr::map() her bekannt ist. In unserem Fall wollen wir nur die Elemente auslesen; Elemente auslesen erreicht man, in dem man sie mit Namen anspricht, in diesem Fall mit dem Platzhalter .x.

Jedes Element von skipgrams1 ist ein 4*1-Tibble und ist ein Skripgram.

skipgrams1 %>% str()
## List of 17
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "systems" "inc" "is" "trying"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "inc" "is" "trying" "to"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "is" "trying" "to" "collect"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "trying" "to" "collect" "a"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "to" "collect" "a" "debt"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "collect" "a" "debt" "that"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "a" "debt" "that" "is"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "debt" "that" "is" "not"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "that" "is" "not" "mine"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "is" "not" "mine" "not"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "not" "mine" "not" "owed"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "mine" "not" "owed" "and"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "not" "owed" "and" "is"
##  $ : tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##   ..$ word: chr [1:4] "owed" "and" "is" "inaccurate"
##  $ : NULL
##  $ : NULL
##  $ : NULL

Das zweite Skipgram von skipgrams1 enthält, naja, das zweite Skipgram.

skipgrams1[[2]] %>% str()
## tibble [4 Ă— 1] (S3: tbl_df/tbl/data.frame)
##  $ word: chr [1:4] "inc" "is" "trying" "to"

Und so weiter.

Okay, weiter im Programm. Jetzt mappen wir das Erstellen der Skipgrams

safe_mutate <- safely(mutate)
  
out1 <- map2(skipgrams1,
             1:length(skipgrams1),
             ~ safe_mutate(.x, window_id = .y))
  
out1 %>% 
  head(2) %>% 
  str()
## List of 2
##  $ :List of 2
##   ..$ result: tibble [4 Ă— 2] (S3: tbl_df/tbl/data.frame)
##   .. ..$ word     : chr [1:4] "systems" "inc" "is" "trying"
##   .. ..$ window_id: int [1:4] 1 1 1 1
##   ..$ error : NULL
##  $ :List of 2
##   ..$ result: tibble [4 Ă— 2] (S3: tbl_df/tbl/data.frame)
##   .. ..$ word     : chr [1:4] "inc" "is" "trying" "to"
##   .. ..$ window_id: int [1:4] 2 2 2 2
##   ..$ error : NULL

out1 ist eine Liste mit 17 Elementen; jedes Element mit jeweils zwei Elementen: Den Ergebnissen und ob es einen Fehler gab bei safe_mutate. Die 10 Elemente entsprechen den 10 Skipgrams. Wir können aber out1 auch “drehen”, transponieren genauer gesagt. so dass wir eine Liste mit zwei Elementen bekommen: das erste Element hat die (zehn) Ergebnisse (nämlich die Skipgrams) und das zweite Elemente, ob es Fehler gab.

Das Prinzip des Transponierens ist in Abbildung fig-Matrix-transpose dargestellt.

Abbildung 7.2: Transponieren einer Matrix (“Tabelle”) 
out2 <-
out1 %>%
  transpose()

Puh, das ist schon anstrengendes Datenyoga…

Aber jetzt ist es einfach. Wir ziehen das erste der beiden Elemente, die Ergebnisse heraus (pluck), entfernen leere Elemente (compact) und machen einen Tibble daraus (bind_rows):

out2 %>% 
  pluck("result") %>%
  compact() %>%
  bind_rows() %>% 
  head()

Geschafft!

7.3.4 Ă„hnlichkeit berechnen

Nachdem wir jetzt slide_windows kennen, schauen wir uns die nächsten Schritte an:

tidy_pmi1 <- nested_words3 %>%  # <--- Kleiner Datensatz!
  mutate(words = future_map(  # Schleife (mit mehreren Kernen) ĂĽber ...
    words,   #  alle Wörter
    slide_windows,  # wobei jedes Mal diese Funtion angewendet wird
    4L  # Parameter an `slide_windows`: Window-Größe ist 4 (L wie "Long", für Integer)
  ))

Wir werden slide_windows auf die Liste words an, die die Beschwerden enthält. Für jede Beschwerde erstellen wir die Skipgrams; diese Schleife wird realisiert über map bzw. future_map, die uns erlaubt, mehrere Kerne des Rechners gleichzeitig zu nutzen, damit es schneller geht.

Hier sehen wir z.B. die Skipgram-IDs der ersten Beschwerde.

tidy_pmi1[["words"]][[1]] %>% 
  head()

Genestet siehst es so aus:

tidy_pmi1 %>% 
  head(1)

Die Listenspalte entschachteln wir mal:

tidy_pmi2 <- tidy_pmi1 %>% 
  unnest(words)  # entschachtele

tidy_pmi2 %>% 
  head()

Zum Berechnen der Ähnlichkeit brauchen wir eineindeutige IDs, nach dem Prinzip “1. Skipgram der 1. Beschwerde” etc:

tidy_pmi3 <- tidy_pmi2 %>% 
  unite(window_id, complaint_id, window_id)  # fĂĽhre Spalten zusammen

tidy_pmi3 %>% 
  head()

Schließlich berechnen wir die Ähnlichkeit mit pairwise_pmi, das hatten wir uns oben schon mal näher angeschaut:

tidy_pmi4 <- tidy_pmi3 %>% 
  pairwise_pmi(word, window_id)  # berechne Ă„hnlichkeit

tidy_pmi <- tidy_pmi4  # mit dem Objekt arbeiten wir dann weiter

tidy_pmi %>% 
  head()

7.3.5 SVD

Die Singulärwertzerlegung (singular value decomposition, SVD) ist ein Verfahren zur Verringerung der Spaltenzahl (Dimension), vergleichbar zur Faktorenanalyse. Zur Anschaulichkeit - und ohne substanziellen Hintergrund - sei folgendes Beispiel genannt: Die Verben “gehen”, “rennen”, “laufen”, “schwimmen”, “fahren”, “rutschen” könnten zu einer gemeinsamen Dimension, etwa “fortbewegen” reduziert werden. Jedes einzelne der eingehenden Verben erhält eine Zahl von 0 bis 1, das die konzeptionelle Nähe des Verbs zur “dahinterliegenden” Dimension (fortbewegen) quantifiziert; die Zahl nennt man auch die “Ladung” des Items (Worts) auf die Dimension. Sagen wir, wir identifizieren 10 Dimensionen. Man erhält dann für jedes unique Wort im Corpus einen Vektor mit den Ladungen auf die Dimensionen. Im genannten Beispiel wäre es ein 10-stelliger Vektor. So wie ein 3-stelliger Vektor die Position einer Biene im Raum beschreibt1, beschreibt hier unser 10-stelliger Vektor die “Position” eines Worts in unserem Einbettungsvektor.

Die Syntax dazu ist dieses Mal einfach:

tidy_word_vectors <- 
  tidy_pmi %>%
  widely_svd(
    item1, item2, pmi,
    nv = 100
  )

tidy_word_vectors %>% 
  (head)

Mit nv = 100 haben wir die Anzahl (n) der Dimensionen (Variablen, v) auf 100 bestimmt.

7.3.6 Wortähnlichkeit

Jetzt, da wir mit der SVD jedes Wort in einem Koordinatensystem verortet haben, können wir die Abstände der Wörter im Koordinatensystem bestimmen. Das geht mit Hilfe des alten Pythagoras, s. Abbildung fig-euklid-distance. Der Abstand, den man mit Hilfe des Satz des Pythagoras berechnet, nennt man auch euklidische Distanz.

Abbildung 7.3: Euklidische Distanz in 2D, Quelle: Wikipedia, CC BY4.0, Kmhkmh

Okay, wir sind in einem Raum mit vielen Dimensionen, was mein Hirn nicht mitmacht, aber der Algebra ist das egal. Pythagoras’ Satz lässt sich genauso anwenden, wenn es mehr als Dimensionen sind.

Die Autoren basteln sich selber eine Funktion in Kap. 5.3, aber der Einfachheit halber nehme ich (erstmal) die entsprechende Funktion aus widyr:

word_neighbors <- 
tidy_word_vectors %>% 
  pairwise_dist(item1, dimension, value)

word_neighbors %>% 
  head()

Schauen wir uns ein Beispiel an. Was sind die Nachbarn von “inaccurate”?

word_neighbors %>% 
  filter(item1 == "inaccurate") %>% 
  arrange(distance) %>% 
  head()

Hier ist die Datenmenge zu klein, um vernünftige Schlüsse zu ziehen. Aber “incorrectly”, “correct”, “balance” sind wohl plausible Nachbarn von “inaccurate”.

7.3.7 Cosinus-Ă„hnlichkeit

Die Nähe zweier Vektoren lässt sich, neben der euklidischen Distanz, auch z.B. ĂĽber die Cosinus-Ă„hnlichkeit (Cosine similarity) berechnen, vgl. auch Abbildung fig-dotproduct:

Abbildung 7.4: Die Cosinus-Ă„hnlichkeit zweier Vektoren

Quelle: Mazin07, Lizenz: PD

\[{\displaystyle {\text{Cosinus-Ă„hnlichkeit}}=S_{C}(A,B):=\cos(\theta )={\mathbf {A} \cdot \mathbf {B} \over \|\mathbf {A} \|\|\mathbf {B} \|}={\frac {\sum \limits _{i=1}^{n}{A_{i}B_{i}}}{{\sqrt {\sum \limits _{i=1}^{n}{A_{i}^{2}}}}{\sqrt {\sum \limits _{i=1}^{n}{B_{i}^{2}}}}}},}\]

wobei \(A\) und \(B\) zwei Vektoren sind und \(\|\mathbf {A} \|\) das Skalarprodukt von A (und B genauso). Das Skalarprodukt von \(\color {red} {a = {\displaystyle [a_{1},a_{2},\cdots ,a_{n}]}}\) und \(\color {blue} {b = {\displaystyle [b_{1},b_{2},\cdots ,b_{n}]}}\) ist so definiert:

\[{\displaystyle \mathbf {\color {red}a} \cdot \mathbf {\color {blue}b} =\sum _{i=1}^{n}{\color {red}a}_{i}{\color {blue}b}_{i}={\color {red}a}_{1}{\color {blue}b}_{1}+{\color {red}a}_{2}{\color {blue}b}_{2}+\cdots +{\color {red}a}_{n}{\color {blue}b}_{n}}\]

Entsprechend ist die Funktion nearest_neighbors zu verstehen aus Kap. 5.3:

nearest_neighbors <- function(df, token) {
  df %>%
    widely(
      ~ {
        y <- .[rep(token, nrow(.)), ]
        res <- rowSums(. * y) / 
          (sqrt(rowSums(. ^ 2)) * sqrt(sum(.[token, ] ^ 2)))
        
        matrix(res, ncol = 1, dimnames = list(x = names(res)))
      },
      sort = TRUE
    )(item1, dimension, value) %>%
    select(-item2)
}

Wobei mit widely zuerst noch von der Langform in die Breitform umformatiert wird, da die Breitform von der Formel verlangt wird bzw. das Rechnen einfacher macht.

Der eine Vektor ist das Embedding des Tokens, der andere Vektor ist das mittlere Embedding über alle Tokens des Corpus. Wenn die Anzahl der Elemente konstant bleibt, kann man sich das Teilen durch \(n\) schenken, wenn man einen Mittelwert berechnen; so hält es auch die Syntax von nearest_neighbors.

Ein nĂĽtzlicher Post zur Cosinus-Ă„hnlichkeit findet sich hier. Dieses Bild zeigt das Konzept der Cosinus-Ă„hnlichkeit anschaulich.

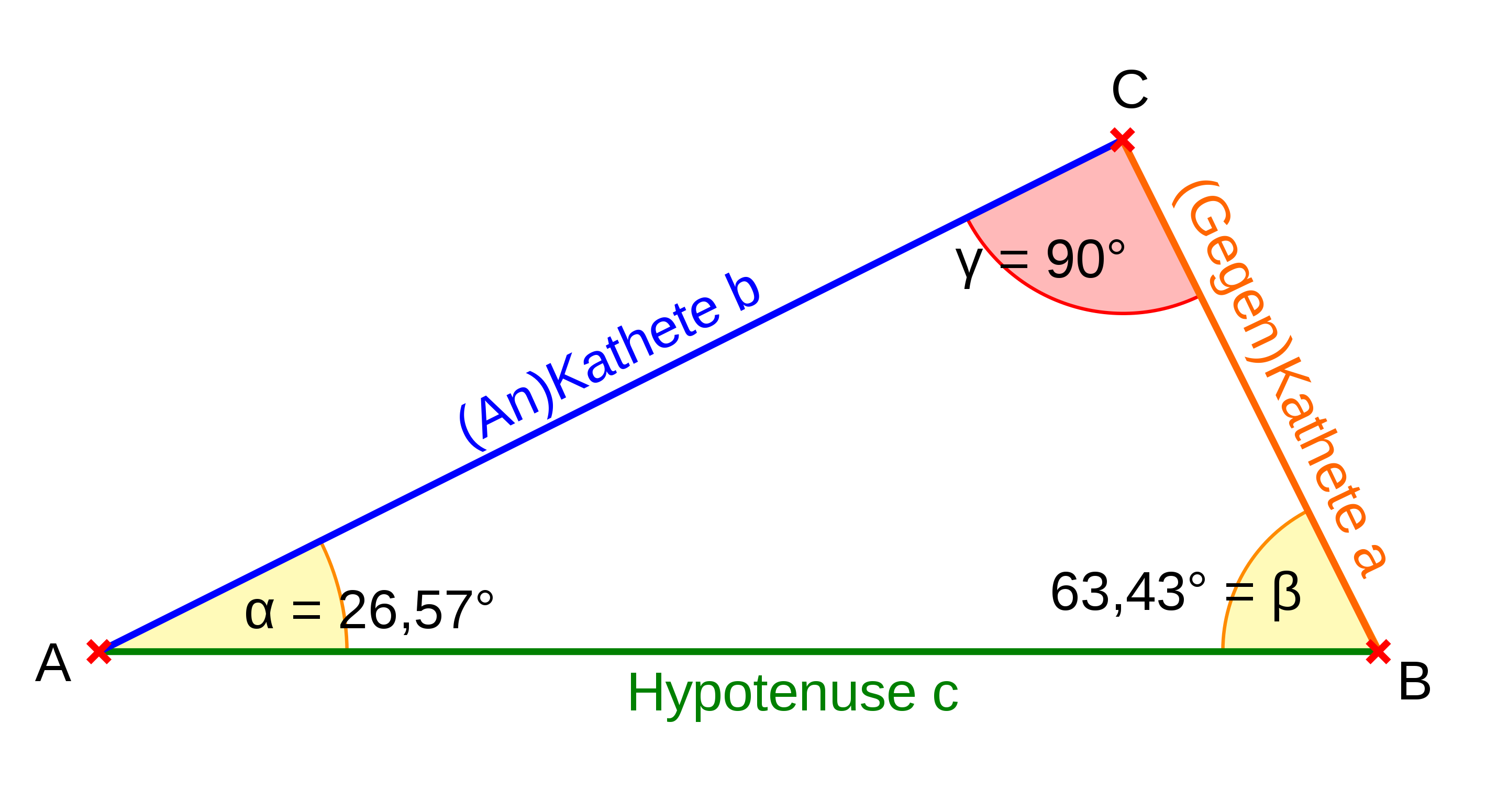
Zur Erinnerung: Der Cosinus eines Winkels ist definiert als Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse2 in einem rechtwinkligen, vgl. Abbildung fig-dreieck.

Abbildung 7.5: Ein rechtwinkliges Dreieck als Grundlage der trigonometrischen Funktionen

Also: \({\displaystyle \cos \alpha ={\frac {b}{c}}}\)

Quelle: PaterSigmund, Wikipedia,dre CC-BY-SA 2.5

Hilfreich ist auch die Visualisierung von Sinus und Cosinus am Einheitskreis; gerne animiert betrachten.

7.4 Word-Embeddings vorgekocht

7.4.1 Glove6B

In Kap. 5.4 schreiben die Autoren:

If your data set is too small, you typically cannot train reliable word embeddings.

Ein paar Millionen Wörter sollte der Corpus schon enthalten, so die Autoren. Da solche “Worteinbettungen” (word embedings) aufwändig zu erstellen sind, kann man fertige, “vorgekochte” Produkte nutzen.

Glove6B wurde anhand von Wikipedia und anderen Datenquellen erstellt (Pennington, Socher, und Manning 2014).

Hinweis

Die zugehörigen Daten sind recht groß; für glove6b (Pennington, Socher, und Manning 2014) ist fast ein Gigabyte fällig. Sie sollten sich die Daten in einem ruhigen Moment (mit stabiler Internetverbindung) herunterladen und in einem Verzeichnis meiner Wahl abgespeichert (datasets). Da bei mir Download abbrach, als ich embedding_glove6b(dimensions = 100) aufrief, habe ich die Daten manuell heruntergeladen, s.u.

Wie immer, Hilfe fĂĽr eine Funktion bekommt man mit ?fun_name oder interaktiv z.B. in RStudio.

glove6b <- 
  embedding_glove6b(dir = "~/datasets",  # aus dem Paket `textdata`
                    dimensions = 50,  # mit nur 50 Dimensionen
                    manual_download = TRUE)  # ist der Datensatz schon manuell heruntergeladen?
glove6b %>% 
  select(1:5) %>% 
  head()

Die ersten paar Tokens sind:

glove6b$token %>% head(20)
##  [1] "the"  ","    "."    "of"   "to"   "and"  "in"   "a"    "\""   "'s"  
## [11] "for"  "-"    "that" "on"   "is"   "was"  "said" "with" "he"   "as"

In eine Tidyform bringen:

tidy_glove <- 
  glove6b %>%
  pivot_longer(contains("d"),
               names_to = "dimension") %>%
  rename(item1 = token)

head(tidy_glove)

Ganz schön groß:

dim(glove6b)
## [1] 400000     51
object.size(tidy_glove)
## 503834736 bytes

In Megabyte3

object.size(tidy_glove) / 2^20
## 480.5 bytes

Einfacher und genauer geht es so:

pryr::object_size(tidy_glove)
## 503.83 MB
pryr::mem_used()
## 858 MB

Um Speicher zu sparen, könnte man glove6b wieder direkt löschen, wenn man nur mit der Tidyform weiterarbeitet.

rm(glove6b)

Jetzt können wir wieder nach Nachbarn fragen, im euklidischen Sinne, wie oben. Probieren wir aus, welche Wörter nah zu “inaccurate” stehen.

Hinweis

Wie wir oben gesehen haben, ist der Datensatz riesig4, was die Berechnungen (zeitaufwändig) und damit nervig machen können. Darüber hinaus kann es nötig sein, dass Sie mehr Speicher auf Ihrem Computer zur Verfügung stellen müssen5. Wir müssen noch maximum_size = NULL, um das Jonglieren mit riesigen Matrixen zu erlauben. Möge der Gott der RAMs und Arbeitsspeicher uns gnädig sein!

Mit pairwise_dist dauert die Berechnung sehr lange und braucht wohl sehr viel Speicher. Mitunter kam folgender Fehler auf: “R error: vector memory exhausted (limit reached?)”.

word_neighbors_glove6b <- 
tidy_glove %>% 
  slice_head(prop = .1) %>% 
  pairwise_dist(item1, dimension, value, maximum_size = NULL)

head(word_neighbors_glove6b)

tidy_glove %>% 
  filter(item1 == "inaccurate") %>% 
  arrange(-value) %>% 
  slice_head(n = 5)

Deswegen probieren wir doch die Funktion nearest_neighbors, so wie es im Buch vorgeschlagen wird, s. Kap 5.3.

nearest_neighbors <- function(df, token) {
  df %>%
    widely(
      ~ {
        y <- .[rep(token, nrow(.)), ]
        res <- rowSums(. * y) / 
          (sqrt(rowSums(. ^ 2)) * sqrt(sum(.[token, ] ^ 2)))
        matrix(res, ncol = 1, dimnames = list(x = names(res)))
      },
      sort = TRUE,
      maximum_size = NULL
    )(item1, dimension, value) %>%
    select(-item2)
}
tidy_glove %>%
  # slice_head(prob = .1) %>% 
  nearest_neighbors("error") %>% 
  head()

Entschachteln wir unsere Daten zu complaints:

tidy_complaints3 <-
  nested_words3 %>% 
  unnest(words)

Dann erstellen wir uns eine Tabelle, in der nur die Schnittmenge der Wörter aus den Beschwerden und Glove vorkommen. Dazu nutzen winr einen inneren Join

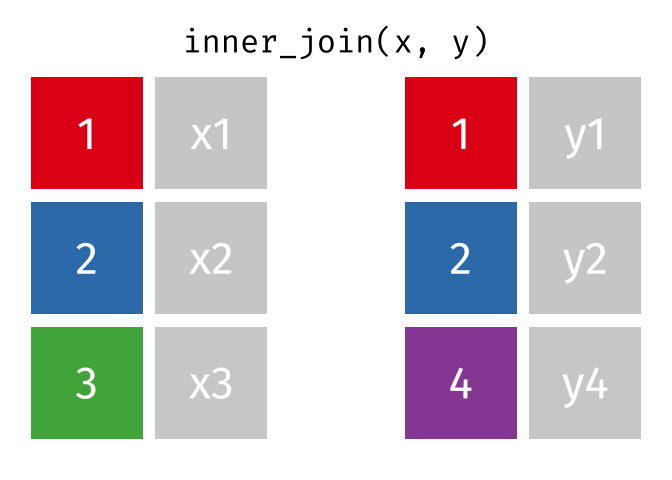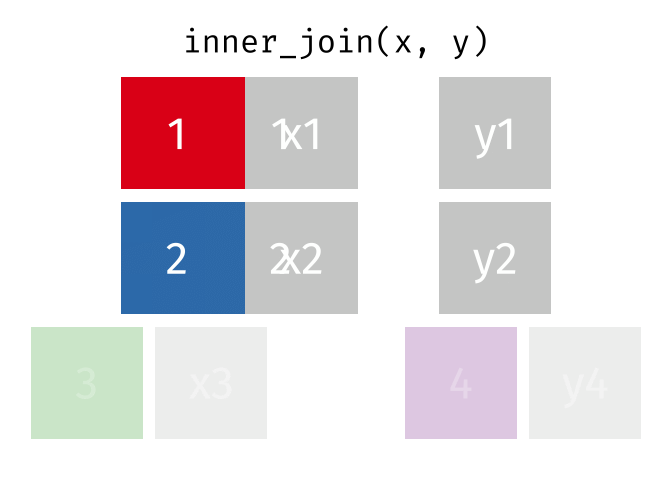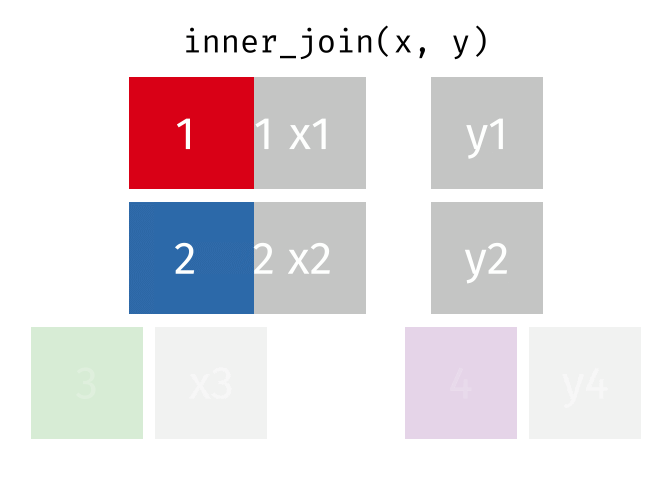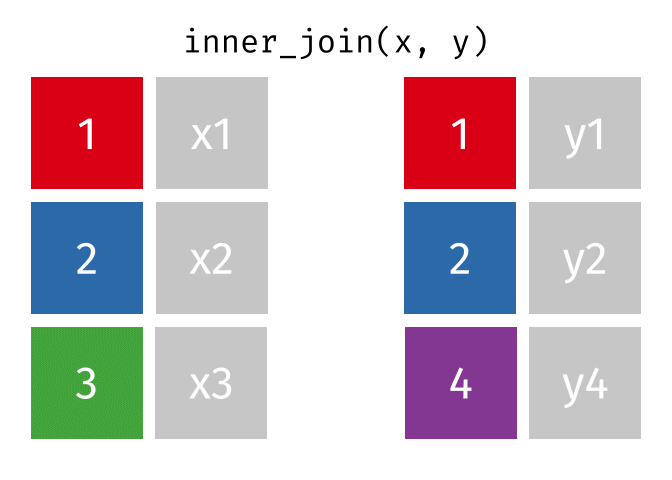
Inner Join, Quelle: Garrick Adenbuie

Quelle

complaints_glove <- 
tidy_complaints3 %>% 
  inner_join(by = "word", 
  tidy_glove %>% 
  distinct(item1) %>% 
  rename(word = item1)) 

head(complaints_glove)

Wie viele unique (distinkte) Wörter gibt es in unserem Corpus?

tidy_complaints3_distinct_words_n <- 
tidy_complaints3 %>% 
  distinct(word) %>% 
  nrow()

tidy_complaints3_distinct_words_n
## [1] 222

In tidy_complaints gibt es übrigens 222 verschiedene Wörter.

word_matrix <- tidy_complaints3 %>%
  inner_join(by = "word",
             tidy_glove %>%
               distinct(item1) %>%
               rename(word = item1)) %>%
  count(complaint_id, word) %>%
  cast_sparse(complaint_id, word, n)

#word_matrix

word_matrix zählt für jede der 10 Beschwerden, welche Wörter (und wie häufig) vorkommen.

dim(word_matrix)
## [1]  10 222

10 Beschwerden (Dokumente) und 222 unique Wörter.

glove_matrix <- tidy_glove %>%
  inner_join(by = "item1",
             tidy_complaints3 %>%
               distinct(word) %>%
               rename(item1 = word)) %>%
  cast_sparse(item1, dimension, value)

#glove_matrix

glove_matrix gibt fĂĽr jedes unique Wort den Einbettungsvektor an.

dim(glove_matrix)
## [1] 222  50

Das sind 222 unique Wörter und 50 Dimensionen des Einbettungsvektors.

Jetzt können wir noch pro Dokument (10 in diesem Beispiel) die mittlere “Position” jedes Dokuments im Einbettungsvektor ausrechnen. Bildlich gesprochen: Was ist der mittlere Raumpunkt (Zentroid) des Bienenschwarms, wobei eine Biene ein Dokument darstellt und die Raumachsen die Dimensionen des Einbettungsvektors.

Dazu gewichten wir jedes Wort eines Dokuments mit den Ladungen des Einbettungsvektor und summieren diese Terme. Es resultiert eine Matrix mit einem Einbettungsvektor pro Dokument. Diese Matrix können wir jetzt als Prädiktorenmatrix hernehmen.

doc_matrix <- word_matrix %*% glove_matrix
#doc_matrix %>% head()
dim(doc_matrix)
## [1] 10 50

Die Anzahl der Dokumente ist 10 und die Anzahl der Dimensionen (des Einbettungsvektors) ist 50.

7.4.2 Wordembeddings fĂĽr die deutsche Sprache

In dem Github-Projekt “Wikipedia2Vec” finden sich die Materialien für ein deutsches Wordembedding (Yamada und Shindo 2019).

7.5 Fazit

Worteinbettungen sind eine aufwändige Angelegenheit. Positiv gesprochen kann ein Analysti die Muskeln spielen lassen und zeigen, was sie oder er so alles drauf hat. Ist ja schon cooles Zeugs, die Word Embeddings. Es besteht die Chance, dass man mit dieser Methode bessere Vorhersagen erreicht, als mit anderen, einfachen Ansätzen wir Worthäufigkeiten oder tf-idf. Auf der anderen Seite ist es oft sinnvoll, mit einfachen Ansätzen zu starten, und zu sehen, wie weit man kommt. Vielleicht ja weit genug. Natürlich haben Modelle auf Basis von Worthäufigkeiten auch ihre Schwächen: Vor allem ist ihre prädiktive Nützlichkeit nicht immer gegeben und die Datensätze werden schnell sehr groß (viele Spalten).

7.6 Fallstudie

Hacker-News-Einbettungs-Fallstudie (was für ein Word!) – Eine praktische Darstellung der Erstellung von Word-Vektoren rein auf Basis der linearen Algebra.

7.7 Vertiefung

Worteinbettungen sind ein zentrales Thema im NLP; fĂĽr moderne Sprachmodelle sind sie von zentraler Bedeutung. Entsprechend findet sich viel Literatur, z.B. (Liu, Lin, und Sun 2023; George 2022; „Word Embeddings in NLP: A Complete Guide“ 2023; Mikolov u. a. 2013; Camacho-Collados und Pilehvar 2020; Almeida und XexĂ©o 2019; Pilehvar und Camacho-Collados 2021).

Ein Online-Python-Tutorial findet sich z.B. bei TensorFlow.

Almeida, Felipe, und Geraldo Xexéo. 2019. „Word Embeddings: A Survey“. ArXiv, Januar. https://www.semanticscholar.org/paper/Word-Embeddings%3A-A-Survey-Almeida-Xex%C3%A9o/e28e81a8cb6655aebb72357538f7b7a360366a29.
Camacho-Collados, Jose, und Mohammad Taher Pilehvar. 2020. „Embeddings in Natural Language Processing“. In Proceedings of the 28th International Conference on Computational Linguistics: Tutorial Abstracts, 10–15. Barcelona, Spain (Online): International Committee for Computational Linguistics. https://doi.org/10.18653/v1/2020.coling-tutorials.2.
George, Alexandra. 2022. Python Text Mining: Perform Text Processing, Word Embedding, Text Classification and Machine Translation. Delhi: BPB Publications.
Hvitfeldt, Emil, und Julia Silge. 2021. Supervised Machine Learning for Text Analysis in R. 1. Aufl. Boca Raton: Chapman and Hall/CRC. https://doi.org/10.1201/9781003093459.
Liu, Zhiyuan, Yankai Lin, und Maosong Sun, Hrsg. 2023. Representation Learning for Natural Language Processing. Singapore: Springer Nature Singapore. https://doi.org/10.1007/978-981-99-1600-9.
Mikolov, Tomas, Kai Chen, Greg Corrado, und Jeffrey Dean. 2013. „Efficient Estimation of Word Representations in Vector Space“. 6. September 2013. https://doi.org/10.48550/arXiv.1301.3781.
Pennington, Jeffrey, Richard Socher, und Christopher Manning. 2014. „GloVe: Global Vectors for Word Representation“. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), 1532–43. Doha, Qatar: Association for Computational Linguistics. https://doi.org/10.3115/v1/D14-1162.
Pilehvar, Mohammad Taher, und Jose Camacho-Collados. 2021. Embeddings in Natural Language Processing: Theory and Advances in Vector Representations of Meaning. Synthesis Lectures on Human Language Technologies. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-031-02177-0.
„Word Embeddings in NLP: A Complete Guide“. 2023. Turing. 2023. https://www.turing.com/kb/guide-on-word-embeddings-in-nlp.
Yamada, Ikuya, und Hiroyuki Shindo. 2019. „Neural Attentive Bag-of-Entities Model for Text Classification“. In Proceedings of the 23th SIGNLL Conference on Computational Natural Language Learning, 563–73. Association for Computational Linguistics.